To perform calculations and process information, people have created different number systems. Let’s learn the basic number systems commonly used in computers.
1. What is the number system?
The number system is a set of symbols (digit, letter) to represent numbers. Each number system consists of a finite set of digits. The number of digits of each number system is called “base” or “radix”.
The basic number systems in computers are:
- Binary number system – base 2
- Octal number system – base 8
- Decimal number system – base 10
- Hexadecimal number system – base 16
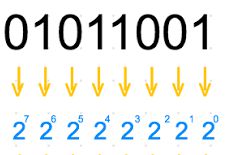
2. Binary number system (base 2)
- Radix 2
- Represented by 2 digits: 0 and 1
- Binary numbers have the form: A(2)=anan-1an-2…a0.a-1a-2…a-m
- The value of A in base 10 is calculated as follows: A(10)=an2n+an-12n-1+an-22n-2+…+a020+a-12-1+a-22-2+…+a-m2-m
- Example: 101(2) = 1.22 + 0.21 + 1.20 = 5(10)
3. Octal number system (base 8)
- Radix 8
- Represented by 8 digits: 0, 1, 2, 3, 4, 5, 6, 7
- Octal numbers have the form: A(8)=anan-1an-2…a0.a-1a-2…a-m
- The value of A in base 10 is calculated as follows: A(10)=an8n+an-18n-1+an-28n-2+…+a080+a-18-1+a-28-2+…+a-m8-m
- Example: 43(8) = 4.81 + 3.80 = 35(10)
4. Decimal number system (base 10)
- Radix 10
- Represented by 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Decimal numbers have the form: A(10)=anan-1an-2…a0.a-1a-2…a-m
- The value of A in base 10 is calculated as follows: A(10)=an10n+an-110n-1+an-210n-2+…+a0100+a-110-1+a-210-2+…+a-m10-m
- Example: 536(10) = 5.102 + 3.101 + 6.100 = 536(10)
5. Hexadecimal number system (base 16)
- Radix 16
- Represented by 16 digits and letters: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. In there, A⟺(equivalent) 10, B⟺11, C⟺12, D⟺13, E⟺14, F⟺15.
- Hexadecimal numbers have the form: A(16)=anan-1an-2…a0.a-1a-2…a-m
- The value of A in base 10 is calculated as follows: A(10)=an16n+an-116n-1+an-216n-2+…+a0160+a-116-1+a-216-2+…+a-m16-m
- Example: 19(16) = 1.161 + 9.160 = 25(10), 1AB(16) = 1.162 + 10.161 + 11.160 = 427(10)
6. Conversion table between radix systems
| Binary | Octal | Decimal | Hexadecimal |
|---|---|---|---|
| 0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
Read more: Convert between basic numbering systems