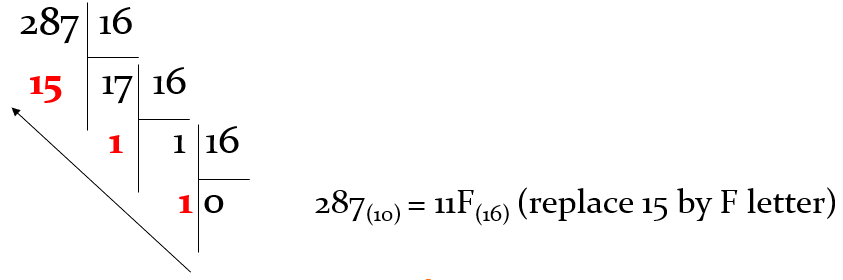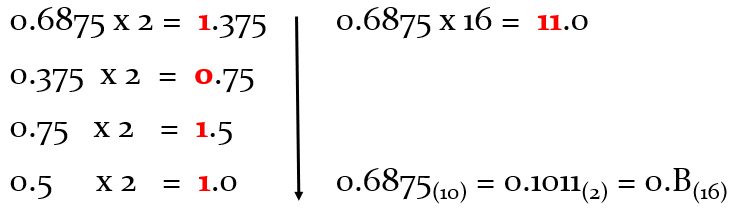This article will help you know how to convert between the number systems. The first thing to pay attention to is how to convert from base 10 to any base system like 2, 8, 16, and vice versa. In addition, how to convert between the base systems 2, 8, and 16 will also be mentioned.
1. Convert base b to base 10
- A(b) = A’(10)
- A’(10) = anbn + an-1bn-1 +…+ a0b0 + a-1b-1 +…+ a-mb-m
- Example:
(6 5 4 3 2 1 0 -1 -2 -3 -4) is the exponent
1 1 0 1 0 0 1 . 1 0 1 1(2)
= 1.26 + 1.25 + 0.24 + 1.23 + 0.22 + 0.21 + 1.20 + 1.2-1 + + 0.2-2 + 1.2-3 + 1.2-4 = 64 + 32 + 8 + 1 + 0.5 + 0.125 + 0.0625 = 105.6875(10)
2. Convert base 10 to base b
To convert the whole-number part of N(10) to base b, follow these steps:
- Divide the whole-number part of N(10) by b to get the quotient and remainder.
- Take the quotient and divide by b to get the next quotient and remainder.
- Repeat the previous step until the quotient is 0.
- The result of the conversion M(b) is the remainder in the division written out in reverse order.
To convert the decimal part of N(10): multiply it by b to get the whole-number part and decimal part after the comma. Then take the decimal part and multiply by b to get the whole-number part and decimal part, repeating this operation until the decimal part is 0. The result of the conversion number M(b) is the integer part numbers in the multiplication, are written in order of multiplication.
3. How to convert between number systems 2, 8, and 16
3.1. Convert from base 2 to base 8
Rule: Gather a sequence of 3 consecutive bits from right to left in base 2 that will correspond to a number in base 8.
Example: 111111111110(2) = ?(8)
Gather 3 bits from right to left (111)(111)(111)(110) to get (7) (7) (7) (6)
Result: 111111111110(2) = 7776(8)
3.2. Convert from base 2 to base 16
Rule: Gather a sequence of 4 consecutive bits from right to left in base 2 that will correspond to a number in base 16.
Example: 11111111111111111110(2) = ?(16)
Gather 4 bits from right to left (1111)(1111)(1111)(1111)(1110) to get (15) (15) (15) (15) (14)
Result: 11111111111111111110(2) = FFFFE(16)
3.3. Convert from base 8 to base 2
Rule: A digit in base 8 will correspond to a sequence of 3 consecutive bits in base 2.
Example: 27(8) = ? (2)
Convert each digit (2) (7) into 3 consecutive bits (010) (111)
Result: 27(8) = 010111(2)
3.4. Convert from base 16 to base 2
Rule: A digit in base 16 will correspond to a sequence of 4 consecutive bits in base 2.
Example: 27(16) = ? (2)
Convert each digit (2) (7) into 4 consecutive bits (0010) (0111)
Result: 27(16) = 00100111(2)
3.5. Convert from base 8 to base 16 and vice versa
The most straightforward way is to convert base 8 to base 2 and then convert to base 16.
Example: 27(8) = ? (16)
Convert each digit (2) (7) into 3 consecutive bits (010) (111). We get binary sequence 010111(2). Convert to base 16 by gathering 4 consecutive bits from right to left (0001)(0111) to get (1)(7).
Result: 27(8) = 00010111(2) = 17(16)